หน่วยการเรียนรู้ที่ 1 เศษส่วนและการบวกลบเสษส่วน
1.การเปรียบเทียบเศษส่วน
2.การบวกเศษส่วนและจำนวนคละ
3.การลบเศษส่วนและจำนวนคละ
4.โจทย์ปัญหาการบวก การลบเศษส่วนและจำนวนคละ
หน่วยการเรียนรู้ที่ 2 การหาร และการบวก ลบ คูณ หารระคนของเศษส่วน
1.การคูณเศษส่วนและจำนวนคละ
2.การหารเศษส่วนและจำนวนคละ
3.การ บวก ลบ คูณ หารระคนเศษส่วนและจำนวนคละ
4.โจทย์ปัญหารการคูณ การหารเศษส่วนและจำนวนคละ
5.โจทย์ปัญหาการบวก ลบ คูณ หารระคนของเศษส่วนและจำนวนคละ
หน่วยการเรียนรู้ที่ 3 ทศนิยมและการบวก การลบทศนิยม
1.ความสัมพันธ์ระหว่างเศษส่วนและทศนิยม
2.การหาค่าประมาณของทศนิมไม่เกินสามตำแหน่ง
3.การบวกและการลบทศนิมยมไม่เกินสามตำแหน่ง
เศษส่วนคืออะไร?
เศษส่วน คือความสัมพันธ์ตามสัดส่วนระหว่างชิ้นส่วนของวัตถุหนึ่งเมื่อเทียบกับวัตถุทั้งหมด เศษส่วนประกอบด้วยตัวเศษ หมายถึงจำนวนชิ้นส่วนของวัตถุที่มี และตัวส่วน หมายถึงจำนวนชิ้นส่วนทั้งหมดของวัตถุนั้น ตัวอย่างเช่น
3
--
4
อ่านว่า เศษสามส่วนสี่ หรือ สามในสี่ หมายความว่า วัตถุสามชิ้นส่วนจากวัตถุทั้งหมดที่แบ่งออกเป็นสี่ส่วนเท่าๆ กัน นอกจากนั้น การแบ่งวัตถุสิ่งหนึ่งออกเป็นศูนย์ส่วนเท่า ๆ กันนั้นเป็นไปไม่ได้ ดังนั้น 0 จึงไม่สามารถเป็นตัวส่วนของเศษส่วนได้
หน่วยการเรียนรู้ที่ 1 เศษส่วนและการบวกลบเสษส่วน
1.การเปรีบยเทียบเศษส่วน
สำหรับการเปรียบเทียบค่าของเศษส่วนนั้น หากตัวส่วนเท่ากันสามารถนำตัวเศษมาเปรียบเทียบกันได้เลย ถ้าส่วนไม่เท่ากันก็นำเศษไปคูณกับส่วนของอีกฝั่งและนำไปคูณทั้งสองจำนวนเหมือนกัน
2.การบวกเศษส่วนและจำนวนคละ
การบวกเศษส่วนและจำนวนคละ ที่มีตัวส่วนไม่เท่ากันต้องทำตัวส่วนให้เท่ากันก่อนแล้วจึงจะหาผลบวกของเศษส่วนและจำนวนคละนั้นคำตอบของเศษส่วน
1.ทำให้เป็นเศษส่วนอย่างต่ำ
2.ถ้าอยู่ในรูปจำนวนคละให้ทำเป็นเศษเกินก่อน
ตัวอย่าง
3.การลบเศษส่วนและจำนวนคละ
การลบเศษส่วนและจำนวนคละ ที่มีตัวส่วนไม่เท่ากันต้องทำตัวส่วนให้เท่ากันก่อนแล้วจึงจะหาผลลบของเศษส่วนและจำนวนคละนั้นคำตอบของเศษส่วน
1.ทำให้เป็นเศษส่วนอย่างต่ำ
2.ถ้าอยู่ในรูปจำนวนคละให้ทำเป็นเศษเกินก่อน
ตัวอย่าง
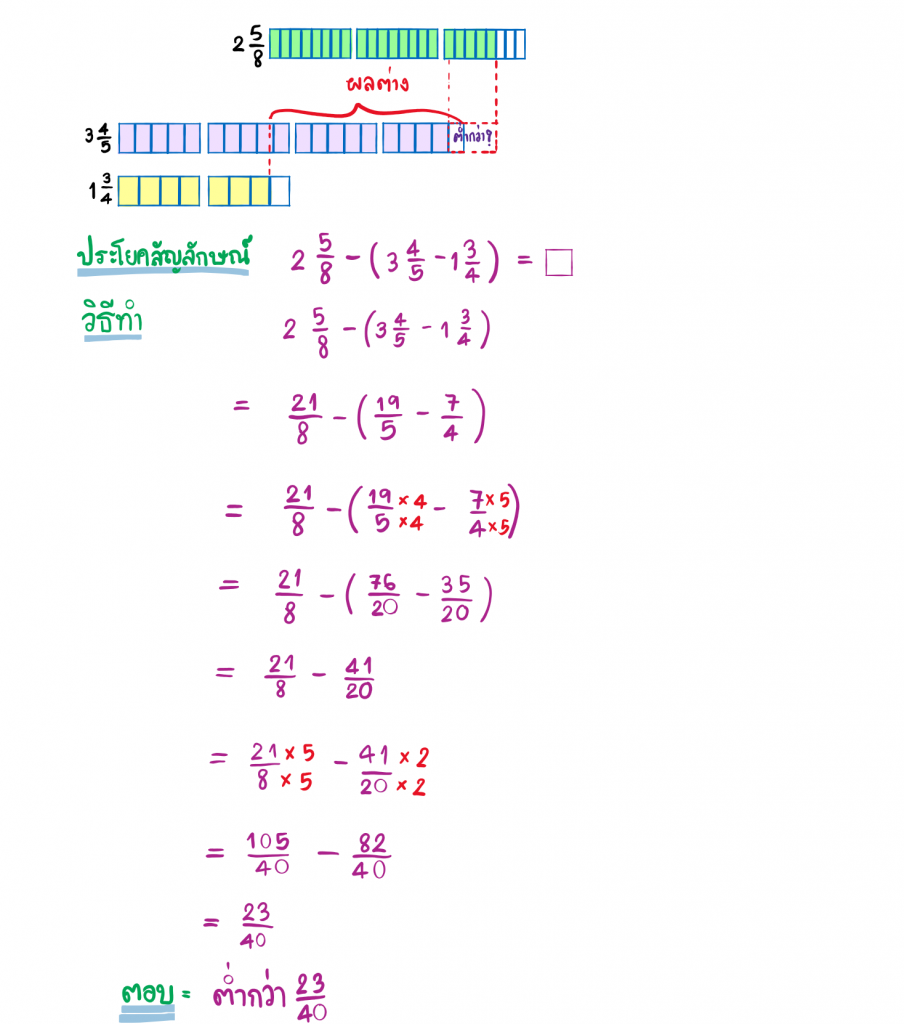
4.โจทย์ปัญหาการบวก การลบเศษส่วนและจำนวนคละ
โจทย์ปัญหาการบวก การลบเศษส่วนและจำนวนคละ ที่มีตัวส่วนไม่เท่ากันต้องทำตัวส่วนให้เท่ากันก่อน
แล้วจึงจะหาผลบวกและลบของเศษส่วนและจำนวนคละนั้น
คำตอบของเศษส่วน
1.ทำให้เป็นเศษส่วนอย่างต่ำ
2.ถ้าอยู่ในรูปจำนวนคละให้ทำเป็นเศษเกินก่อน เช่น
โจทย์ปัญหาการลบเศษส่วน
โจทย์ปัญหาการบวกเศษส่วน

1.การคูณเศษส่วนและจำนวนคละ
1.การคูณจำนวนคละ
1.สมมติว่ากำลังนำ 41/2 มาคูณกับ 62/5
2.แปลงจำนวนคละจำนวนแรกให้เป็นเศษเกิน. เศษเกินคือจำนวนที่ตัวเศษมากกว่าตัวส่วน เราสามารถแปลงจำนวนคละเป็นเศษเกินด้วยขั้นตอนง่ายๆ ดังต่อไปนี้
นำจำนวนเต็มคูณกับตัวส่วนของเศษส่วนนั้น
ถ้าเรากำลังแปลง 41/2 ให้เป็นเศษเกิน เราจะต้องนำ 4 มาคูณกับตัวส่วนของเศษส่วนนั้นซึ่งก็คือ 2 ฉะนั้นจะได้ 4 x 2 = 8
นำผลคูณที่ได้ไปบวกกับตัวเศษของเศษส่วนนั้น
นำ 8 ไปบวก 1 เราก็จะได้ 8 + 1 = 9
นำผลบวกที่ได้ไปวางแทนที่ตัวเศษเดิมของเศษส่วนนั้น
นำผลบวกซึ่งก็คือ 9 ไปวางไว้เหนือเลข 2 แทนตัวเศษเดิม
41/2 แปลงเป็นเศษเกินได้ 9/2
3.แปลงจำนวนคละจำนวนที่สองให้เป็นเศษเกิน. ทำตามขั้นตอนเดียวกับที่ได้อธิบายไปแล้วข้างต้น
นำจำนวนเต็มมาคูณกับตัวส่วนของเศษส่วนนั้น
ถ้ากำลังแปลง 62/5 เป็นเศษเกิน เราจะต้องนำ 6 ไปคูณตัวส่วนของเศษส่วนนั้นซึ่งก็คือ 5 ก็จะได้ 6 x 5= 30
นำผลคูณที่ได้ไปบวกกับตัวเศษของเศษส่วนนั้น
นำ 30 ไปบวก 2 ก็จะได้ 30 + 2 = 32
นำผลบวกที่ได้ไปวางแทนที่ตัวเศษเดิมของเศษส่วนนั้น
ตัวเศษใหม่คือ 32 เราสามารถนำจำนวนนี้ไปวางไว้เหนือ 5 แทนตัวเศษเดิม
62/5 แปลงเป็นเศษเกินได้ 32/5
4.นำเศษเกินทั้งสองมาคูณกัน. พอแปลงจำนวนคละแต่ละจำนวนเป็นเศษเกินแล้ว ก็สามารถนำจำนวนทั้งสองมาคูณกันได้ นำตัวเศษมาคูณกับตัวเศษและนำตัวส่วนมาคูณกับตัวส่วน
เมื่อจะนำ 9/2 มาคูณกับ 32/5 นำตัวเศษมาคูณกับตัวเศษก่อน นั่นคือนำ 9 และ 32 มาคูณกัน ก็จะได้ 9x32=288
ต่อมานำตัวส่วนมาคูณกัน นำ 2 และ 5 มาคูณกัน ก็จะได้ 10
นำเศษตัวใหม่มาวางไว้บนส่วนตัวใหม่ ก็จะได้ 288/10.
5.ทำให้เป็นเศษส่วนอย่างต่ำ. หาตัวหารร่วมมาก (ห.ร.ม.) ที่สามารถหารทั้งตัวเศษและตัวส่วนได้ลงตัวเพื่อทำให้เป็นเศษส่วนอย่างต่ำ เมื่อหาได้แล้ว ให้นำตัวเลขนั้นมาหารทั้งเศษและส่วน
2 เป็นตัวหารร่วมมากที่สามารถหารทั้ง 288 และ 10 ได้ลงตัว 288 หาร 2 ได้ 144 และ 10 หาร 2 ได้ 5
เมื่อทำ 288/10 ให้เป็นเศษส่วนอย่างต่ำก็จะได้ 144/5.
6.แปลงเศษเกินให้เป็นจำนวนคละ. เนื่องจากโจทย์เป็นจำนวนคละ ฉะนั้นคำตอบก็ควรเป็นจำนวนคละเช่นเดียวกัน เราจะต้องทำขั้นตอนย้อนกลับเพื่อจะได้แปลงเศษเกินให้เป็นจำนวนคละได้ วิธีการมีดังนี้นำตัส่วนไปหารตัวเศษก่อนนำ 5 ไปหารยาวกับ 144 ก็จะได้ 28 ฉะนั้นผลหารคือ 28 เศษหรือจำนวนที่เหลืออยู่คือ 4
ทำผลหารให้เป็นจำนวนเต็ม นำเศษที่เหลือจากการหารมาวางแทนที่ตัวเศษเดิมเพื่อเป็นการจบขั้นตอนแปลงเศษเกินให้เป็นจำนวนคละผลหารคือ 28 เหลือเศษ 4 และตัวส่วนเดิมคือ 5 ฉะนั้นเมื่อทำให้ 144/5 เป็นจำนวนคละก็จะได้ 284/5
7.เสร็จสิ้นขั้นตอน!
41/2 x 62/5 = 284/5
1 การหารเศษส่วน
1.กลับเศษส่วนที่เป็นตัวหารและเปลี่ยนเครื่องหมายหารเป็นเครื่องหมายคูณ. สมมติว่าเรากำลังหาร 1/2 ด้วย 18/20 ถ้าเรากลับ 18/20 ก็จะได้ 20/18 และเปลี่ยนเครื่องหมายหารเป็นเครื่องหมายคูณ ฉะนั้นก็จะได้ 1/2 ÷ 18/20 = 1/2 x 20/18
2.ตัวเศษคูณตัวเศษและตัวส่วนคูณตัวส่วนแล้วค่อยทำคำตอบให้เป็นเศษส่วนอย่างต่ำ. ตอนนี้ขั้นตอนที่ต้องทำเหมือนเดิมคือคูณ นำตัวเศษ 1 และ 20 มาคูณกัน ก็จะได้ผลคูณของตัวเศษคือ 20 นำตัวส่วน 2 และ 18 มาคูณกัน ก็จะได้ผลคูณของตัวส่วนคือ 36 ฉะนั้นคำตอบของเศษส่วนที่ได้คือ 20/36 จำนวนที่มากที่สุดซึ่งสามารถหารทั้งตัวเศษและตัวส่วนได้ลงตัวคือ 4 ฉะนั้นหารตัวเศษและตัวส่วนด้วย 4 เพื่อจะได้เศษส่วนอย่างต่ำ 20/36 ÷ 4/4 = 5/9
3.การ บวก ลบ คูณ หารระคนเศษส่วนและจำนวนคละ
1.การคูณเศษส่วนและจำนวนคละ
การคูณเศษส่วนและจำนวนคละ นำตัวเศษคูนตัวส่วน
คำตอบเศษส่วน
1.ทำให้เป็นเศษส่วนอย่างต่ำ
2.ถ้าอยู่ในรูปเศาเกิน ให้ทำเป็นจำนวนคละ
ตัวอย่าง
2.การหารเศษส่วนและจำนวนคละ
สลับเศษส่วน''ตัวหาร''แล้วคูนเหมือนการคูนเศษส่วนโดยการคูนไขว้

3.การ บวก ลบ คูณ หารระคนเศษส่วนและจำนวนคละ
4.โจทย์ปัญหารการคูณ การหารเศษส่วนและจำนวนคละ
5.โจทย์ปัญหาการบวก ลบ คูณ หารระคนของเศษส่วนและจำนวนคละ
หน่วยการเรียนรู้ที่ 3 ทศนิยมและการบวก การลบทศนิยม
1.ความสัมพันธ์ระหว่างเศษส่วนและทศนิยม
2.การหาค่าประมาณของทศนิมไม่เกินสามตำแหน่ง
3.การบวกและการลบทศนิมยมไม่เกินสามตำแหน่ง

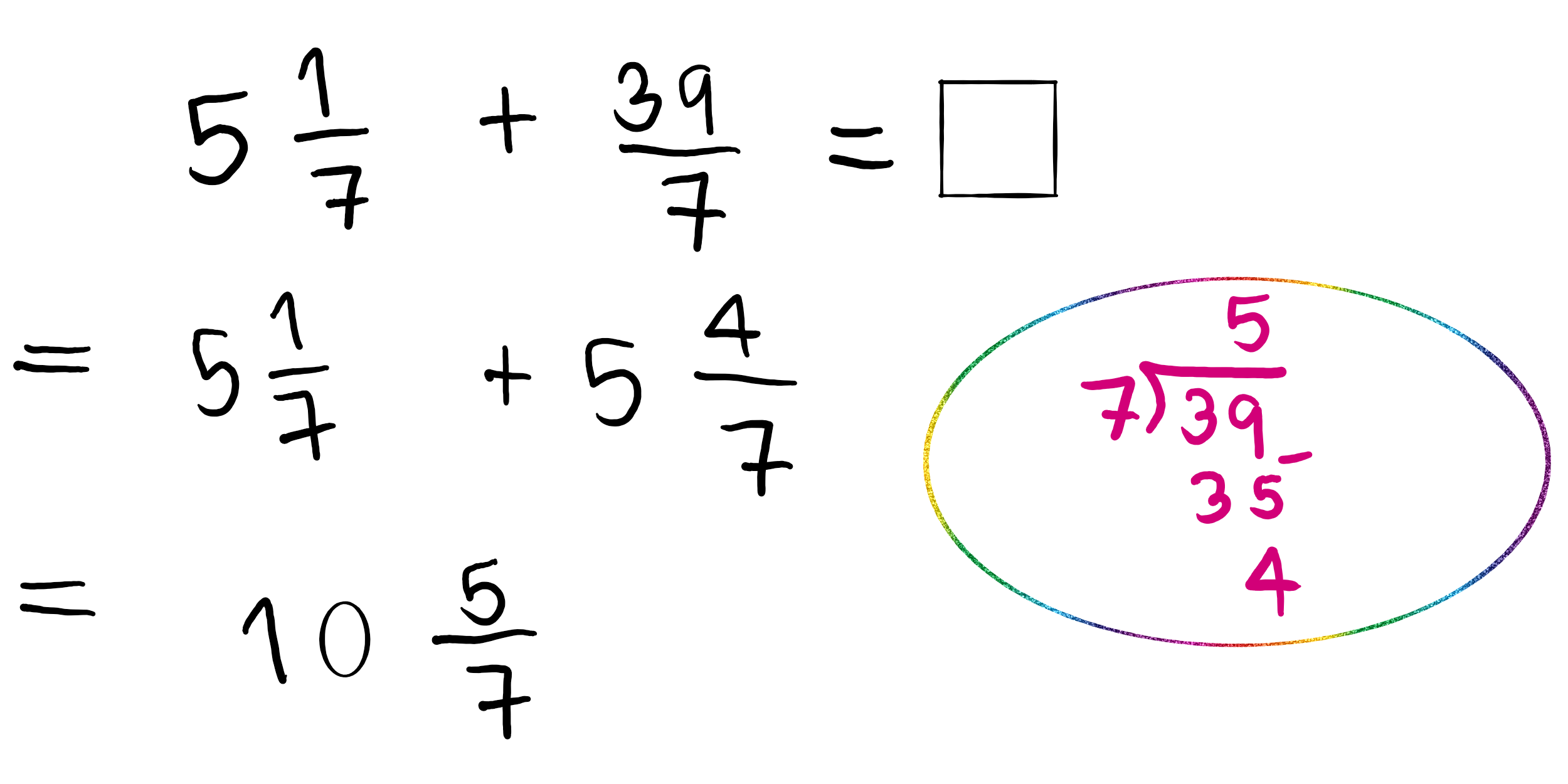
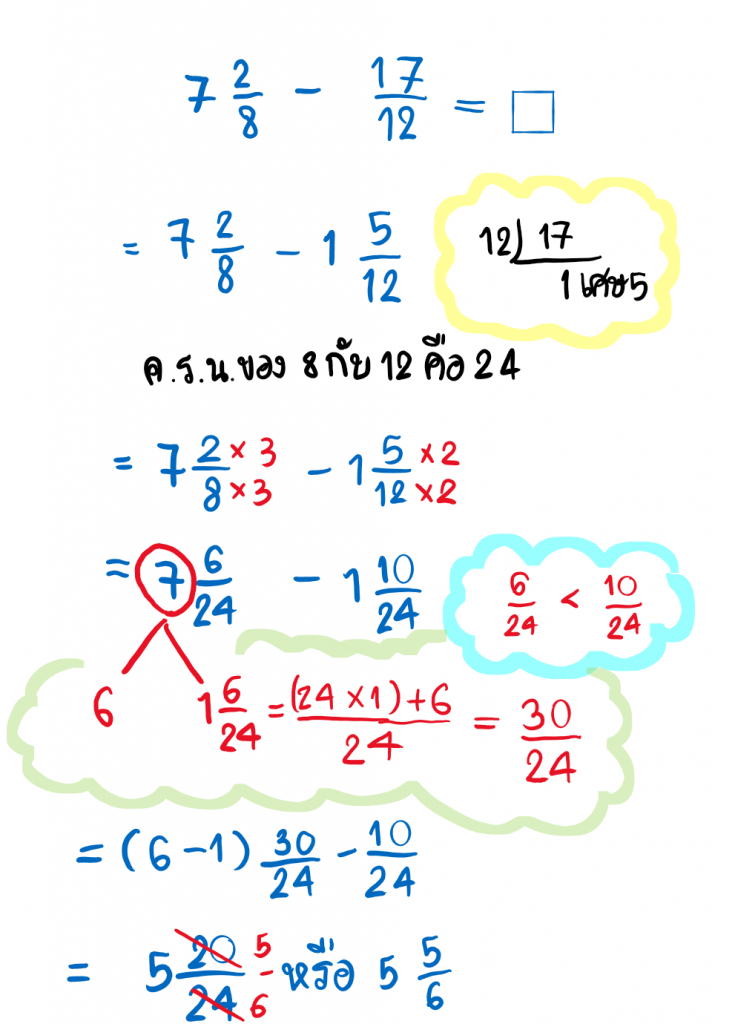

















ไม่มีความคิดเห็น:
แสดงความคิดเห็น